黄圣杰

bjfuhsj.top

Diffusion Model

发表于 更新于 阅读次数：
本文字数： 3.7k 阅读时长 ≈ 3 分钟

Diffussion Model——扩散概率模型

——适用于所有的生成类任务：TTS （☑️）、VC（❓）

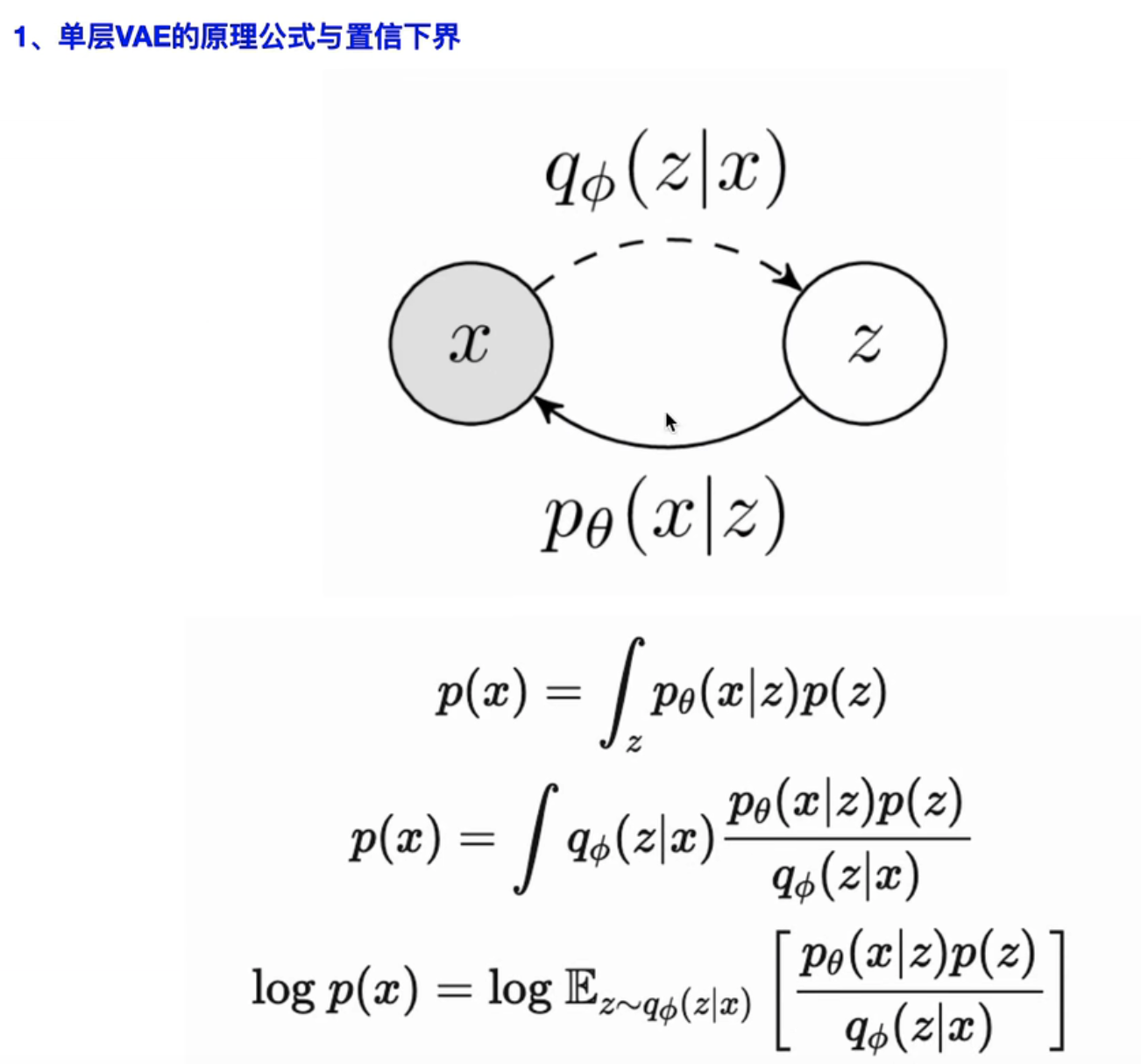
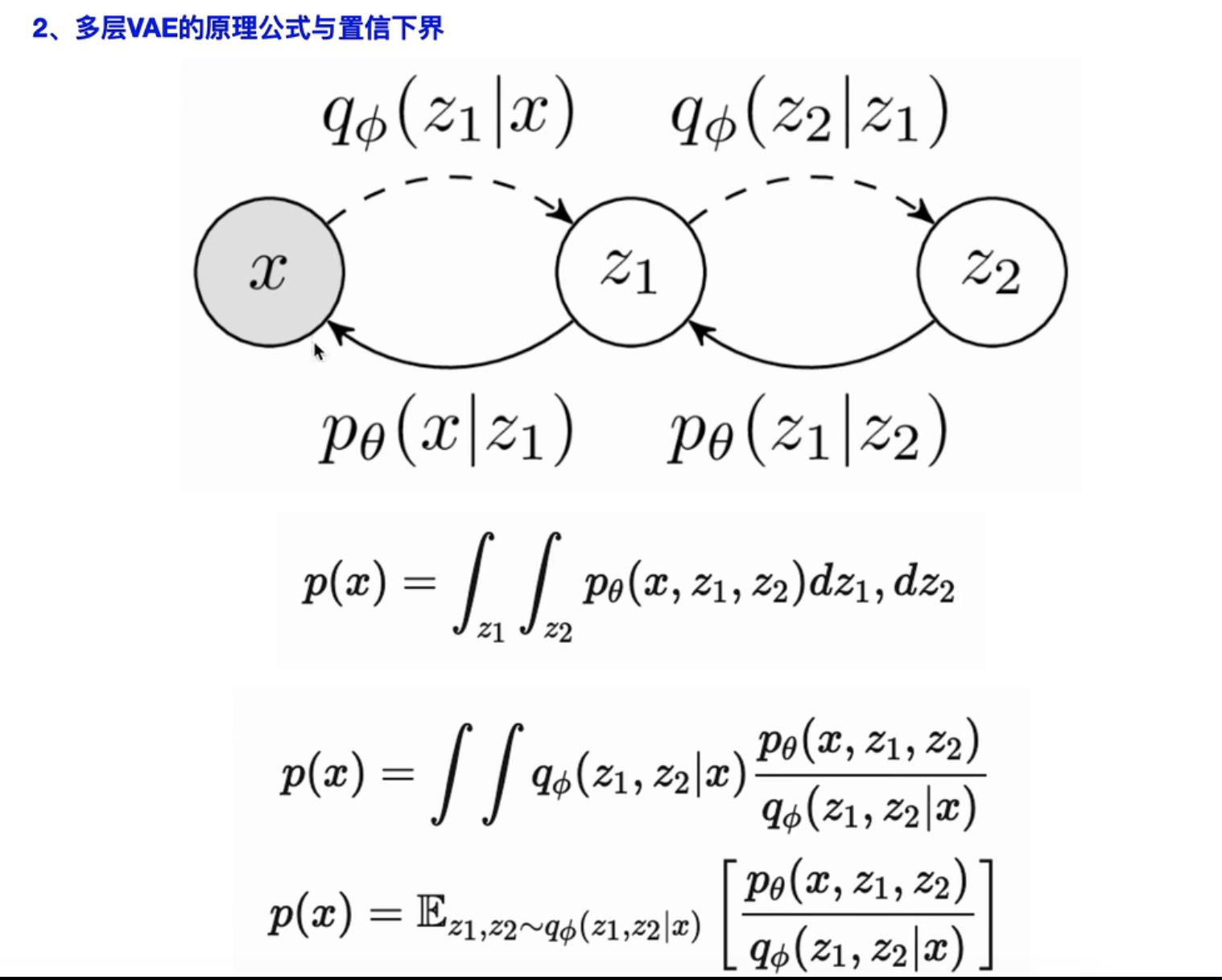
——其实和VAE有点像：多层 VAE

image-20220605112436197

  • 最早见刊时间 1995-2004

  • 论文：2015-ICML && ==2020-NIPS==

    • [1] Ho, Jonathan, Ajay Jain, and Pieter Abbeel. “Denoising diffusion probabilistic models.” Advances in Neural Information Processing Systems 33 (2020): 6840-6851.
    • [2] Sohl-Dickstein, Jascha, et al. “Deep unsupervised learning using nonequilibrium thermodynamics.” International Conference on Machine Learning. PMLR, 2015.

  • github代码

  • 视频解读Bilibili

  • 前置的数学知识

image-20220605143554259

  • 贝叶斯公式
  • VAE：KL散度

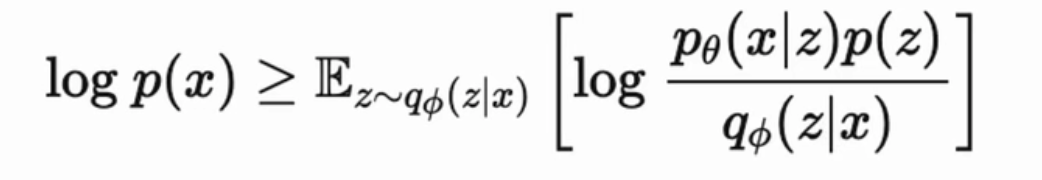
image-20220605144221925)image-20220605151903434

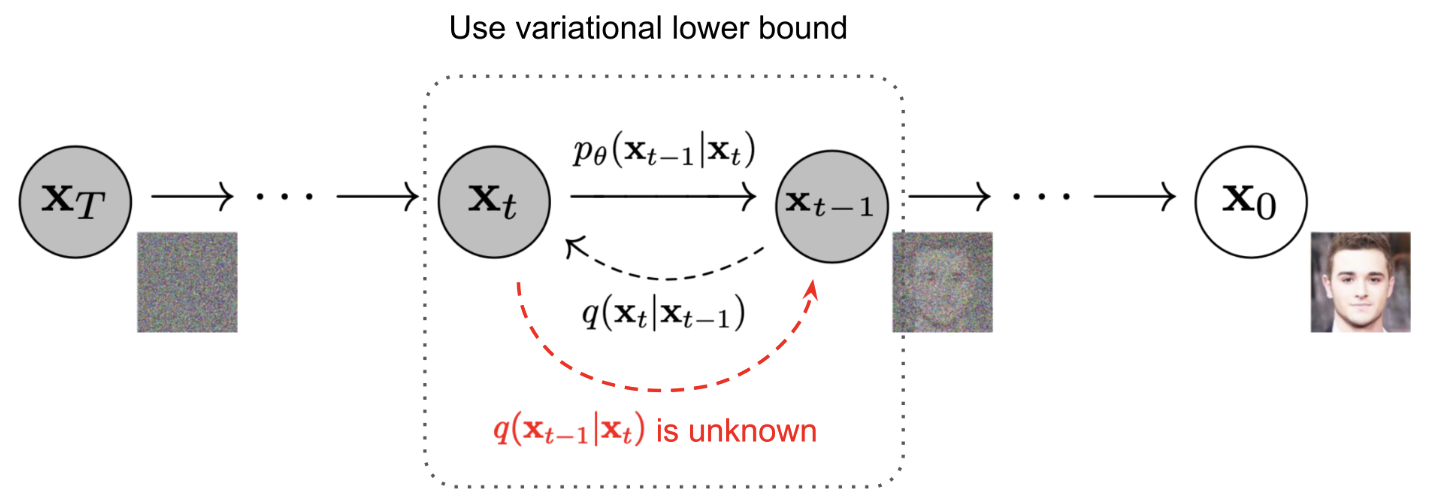
  • 训练：x->z
  • 推理：z->x
  • 【联合概率分布】
  • 训练目标：最大化“对数似然” log p(x)
  • 分子分母同时乘上一个“后验分布” q
  • image-20220605151544252

image-20220605151340796)image-20220605151645670

  • 基于的是 Markvo 假设

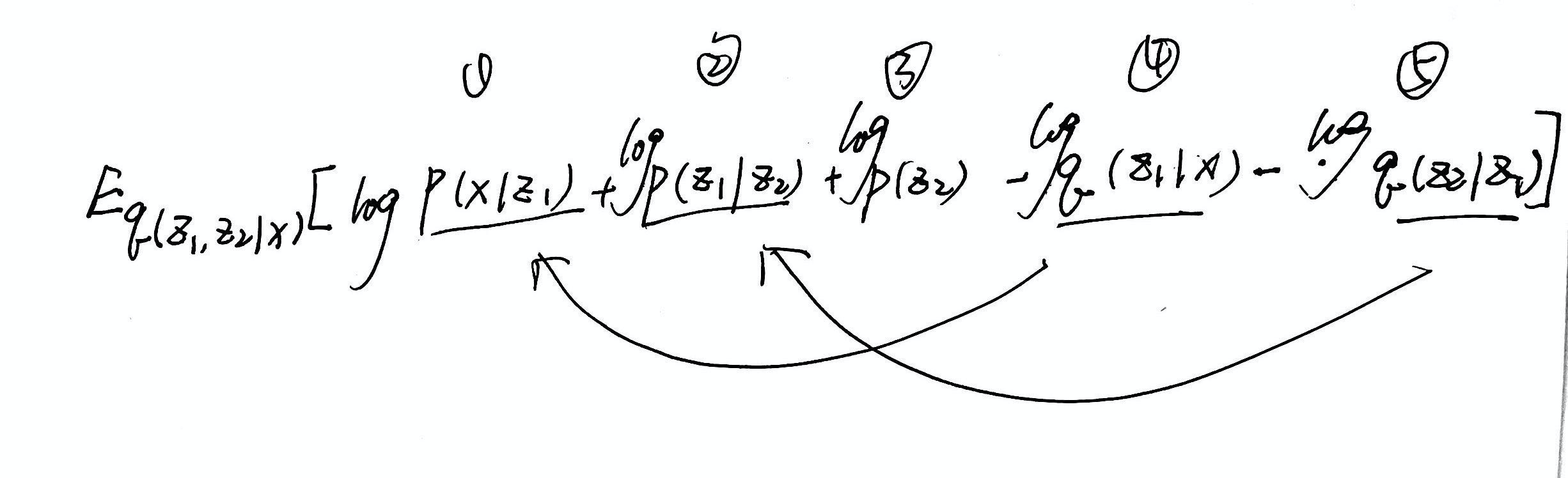
  • image-20220605152702039

❤️思考：Diffusion & Multi-VAE 的区别？

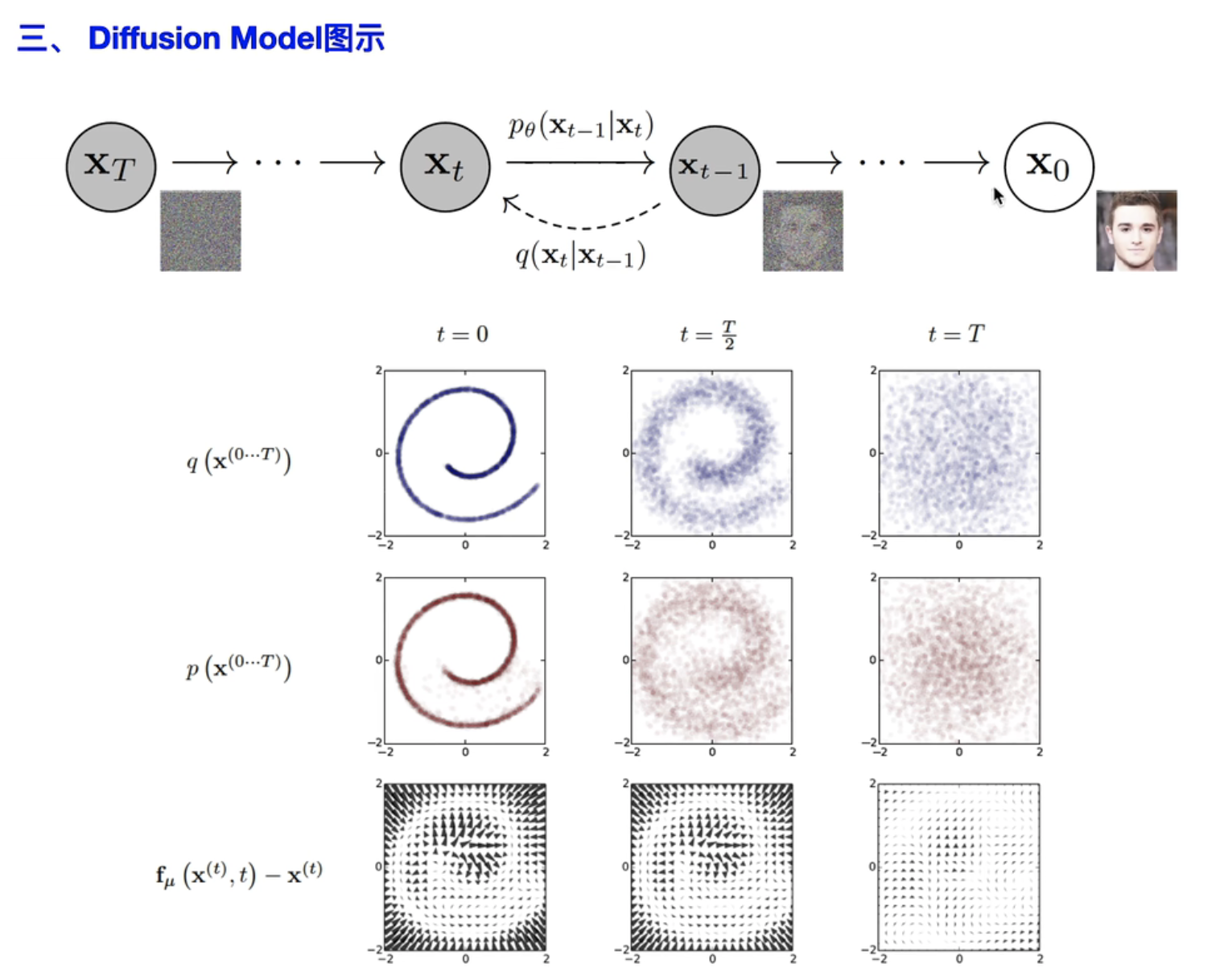
image-20220605152857214

    1. X0->Xt 扩散过程：熵增
    2. Xt->X0 逆扩散：去噪，还原
    3. ：对应的“条件概率分布”

image-20220605153221865

  • ==正向过程不含参数，所有 均值、方差 都是确定的==，是一个 markvo链的关系。类比lr，固定不变
  • 正向加噪的过程，是一个条件概率分布，而且是一个 高斯正太分布，均值为： “$
    \sqrt{1-\beta_{t}} \mathbf{x}{t-1}
    $”，方差为 ：“$\beta    {t}$”
  • 各向独立：“各向同性”

🌟怎么算 X 呢？：

  • image-20220605154232033

  • 然后可以套 Markvo 迭代，不断得到 Xt+1 … 更多采样值

  • 问题：
    • T 理论是 ∞ 无穷大，怎么设置？
    • 参数化分布的 “$\beta_{t}$” （方差）应该怎么设置？
  • $
    \left{\beta_{t} \in(0,1)\right}_{t=1}^{t}
    $
  • 随着时间推移，$\beta_{t}$ 越来越大

关于 T：参数重整化 算出来

image-20220605154836448

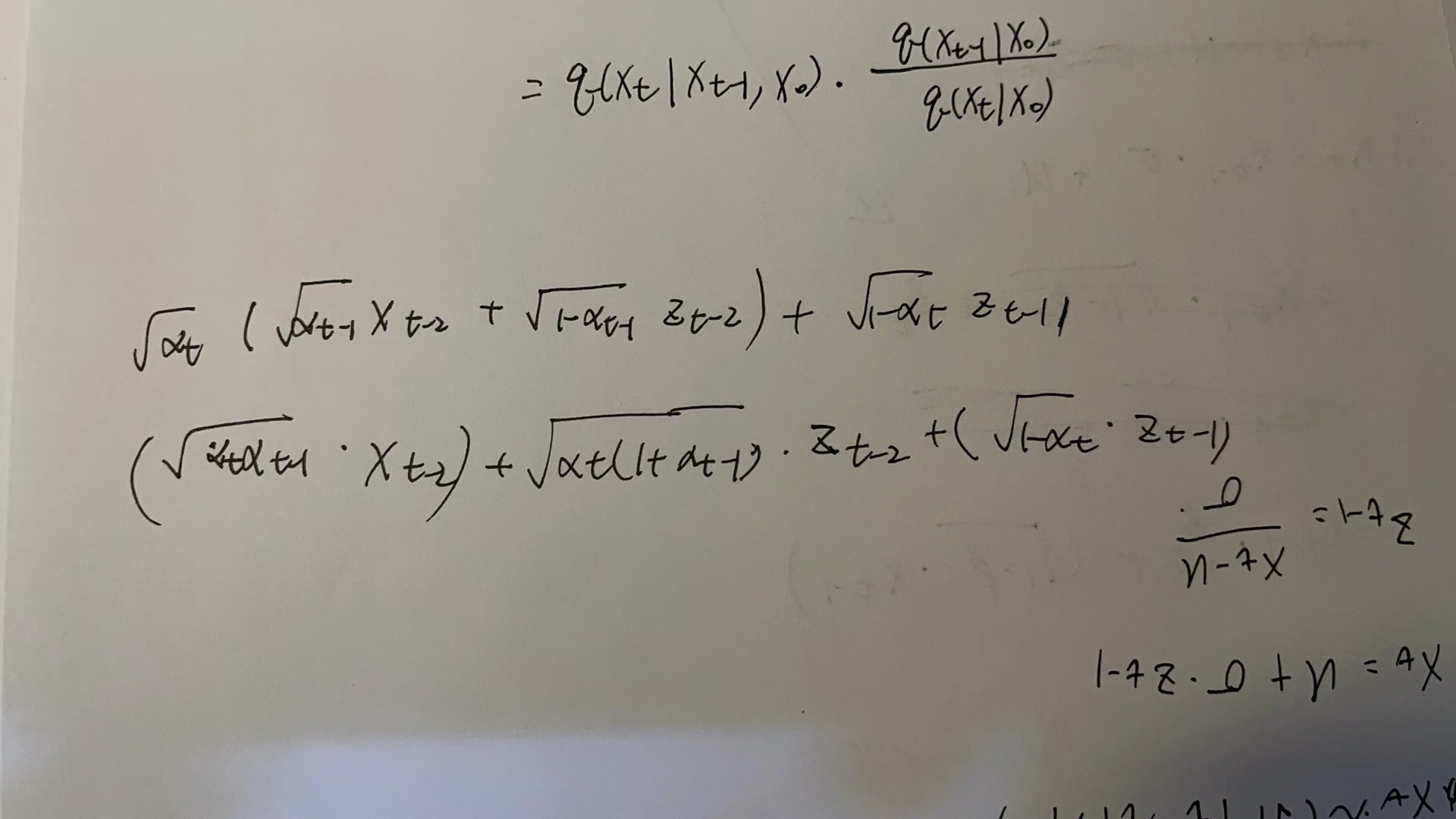
image-20220605180041989

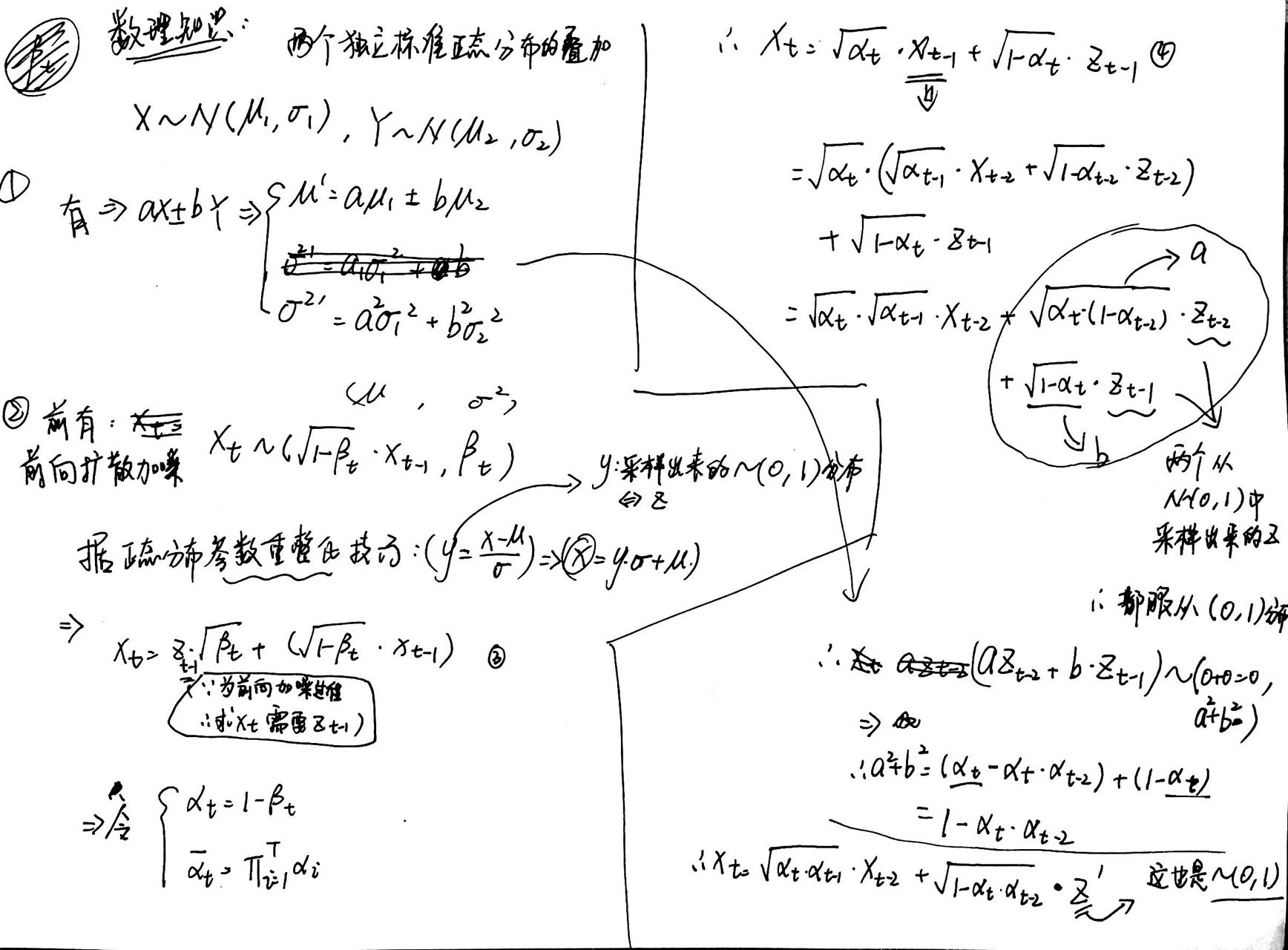
image-20220606000627561

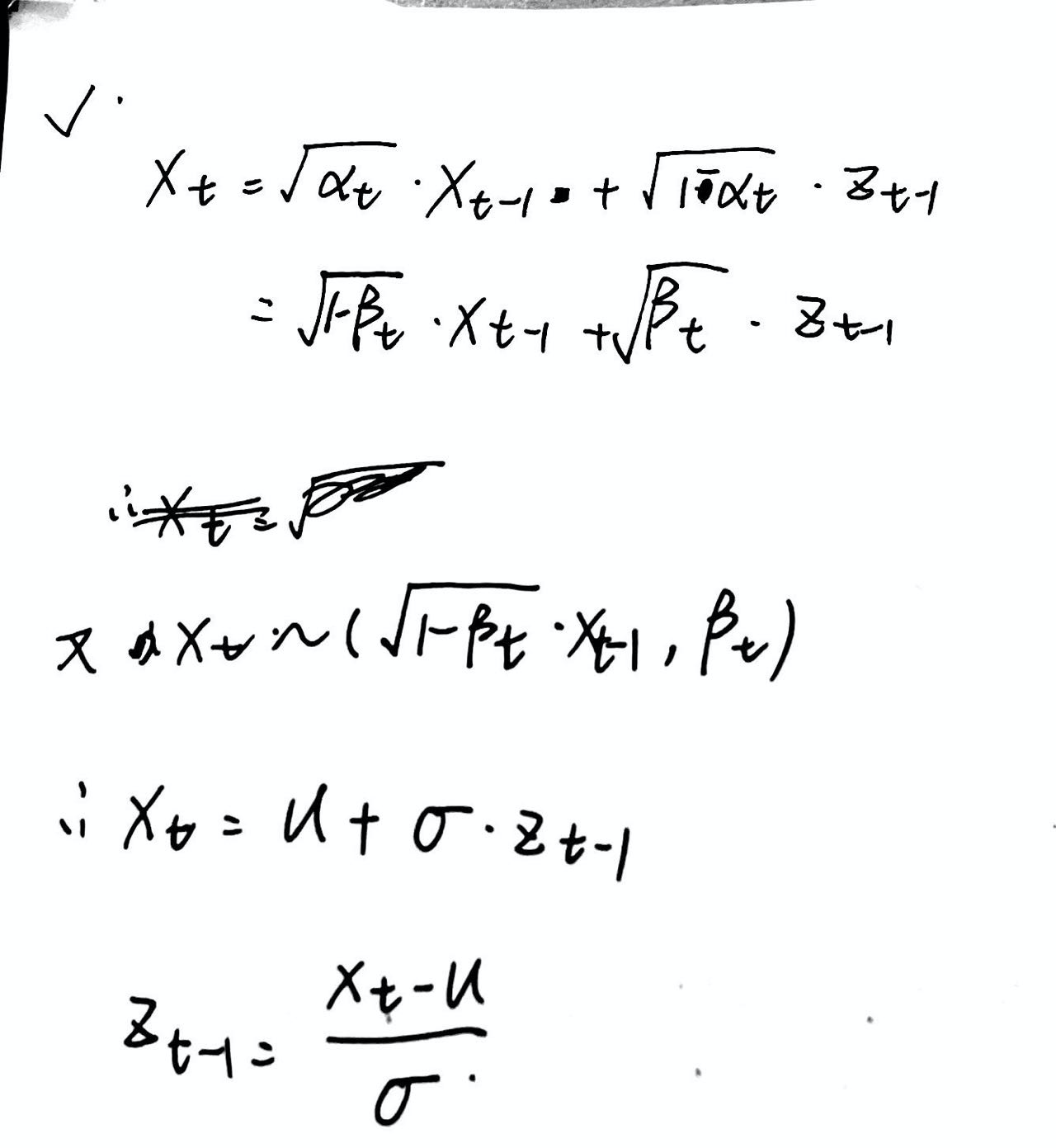
image-20220605160908387

所以：

image-20220605161022505

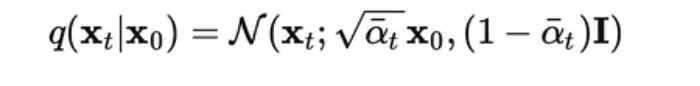
  • 所以，时间取决于：最后的 均值、方差，接近于 “==各向同性==”的正态分布了：即==（0，1）==时，那么就可以说明 Xt “正向扩散过程”已经完全ok了，可以开始“逆扩散过程”了。

  • 这其中，均值方差 alpha、beta （参数化正态分布时设置的）都是我们自己设定的，是个固定值，所以完全可控

  • 总之：==正向扩散，想要得到“标准正态分布”==

  • 一般原则：分布接近噪声时，beta 可以变大，刚开始时，beta 不要太大

🌟逆扩散过程

image-20220605161617915)image-20220605161824972

  • 逆扩散，仍然是一个 Markvo chain 过程
  • 需要构建一个“==参数分布==”：不然直接从 Xt 到 X0 链式求取非常麻烦，所以需要构建一个网络
  • 也是假设为一个 “高斯分布”
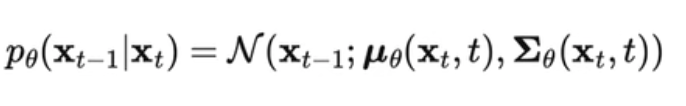
  • image-20220605164735409
  • 把问题转化为 （Xt，t）两个变量的关系网络，均值方差都是和（Xt，t）这两个相关
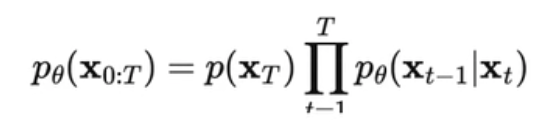
  • image-20220605164854035
  • image-20220605165014152：
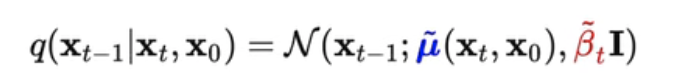
  • image-20220605165127198

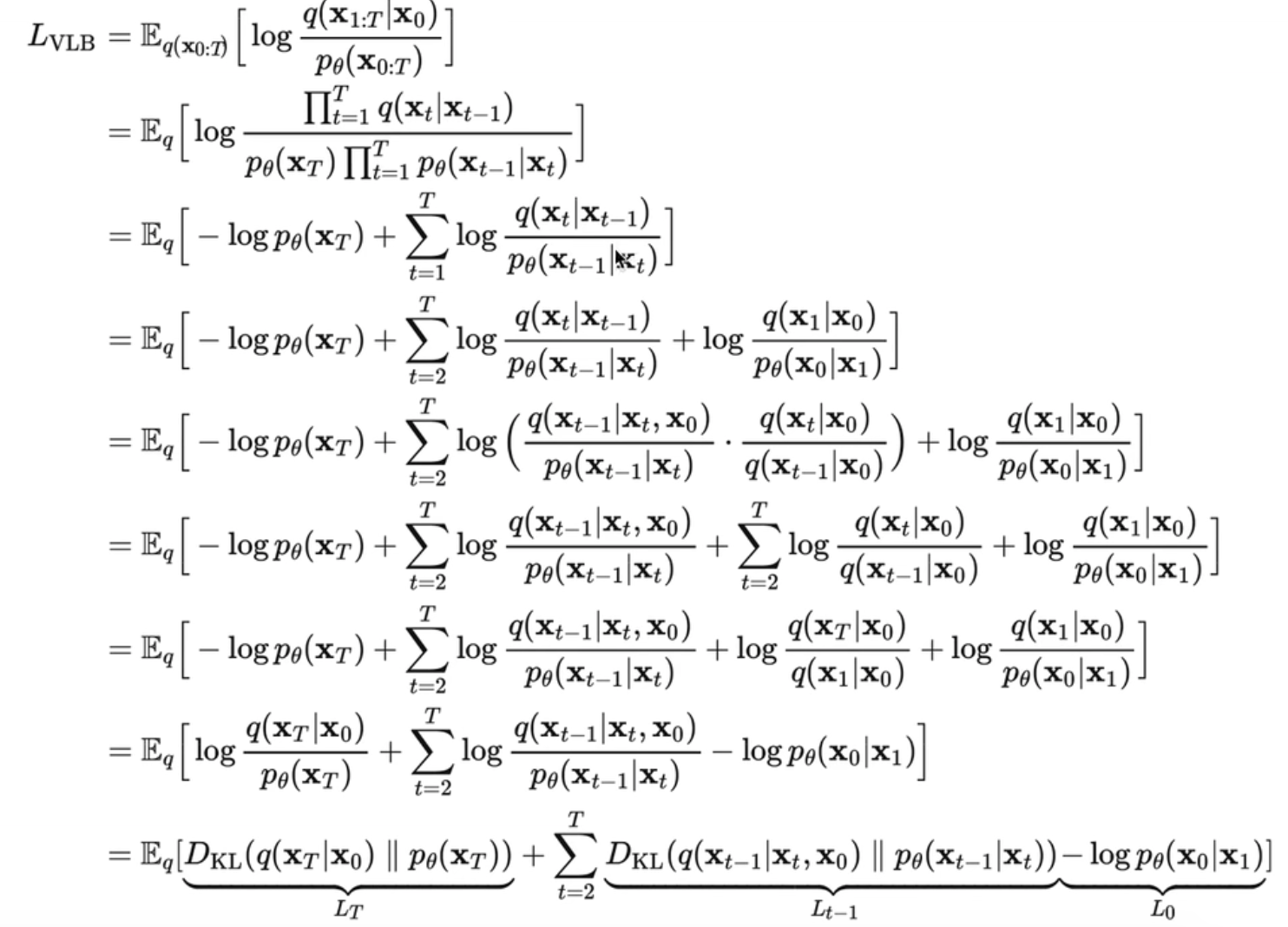
🌟说说怎么算：

image-20220605165947867

==》基于贝叶斯公式：

image-20220605165908200

image-20220605161903503

image-20220605161940198)image-20220605162006080

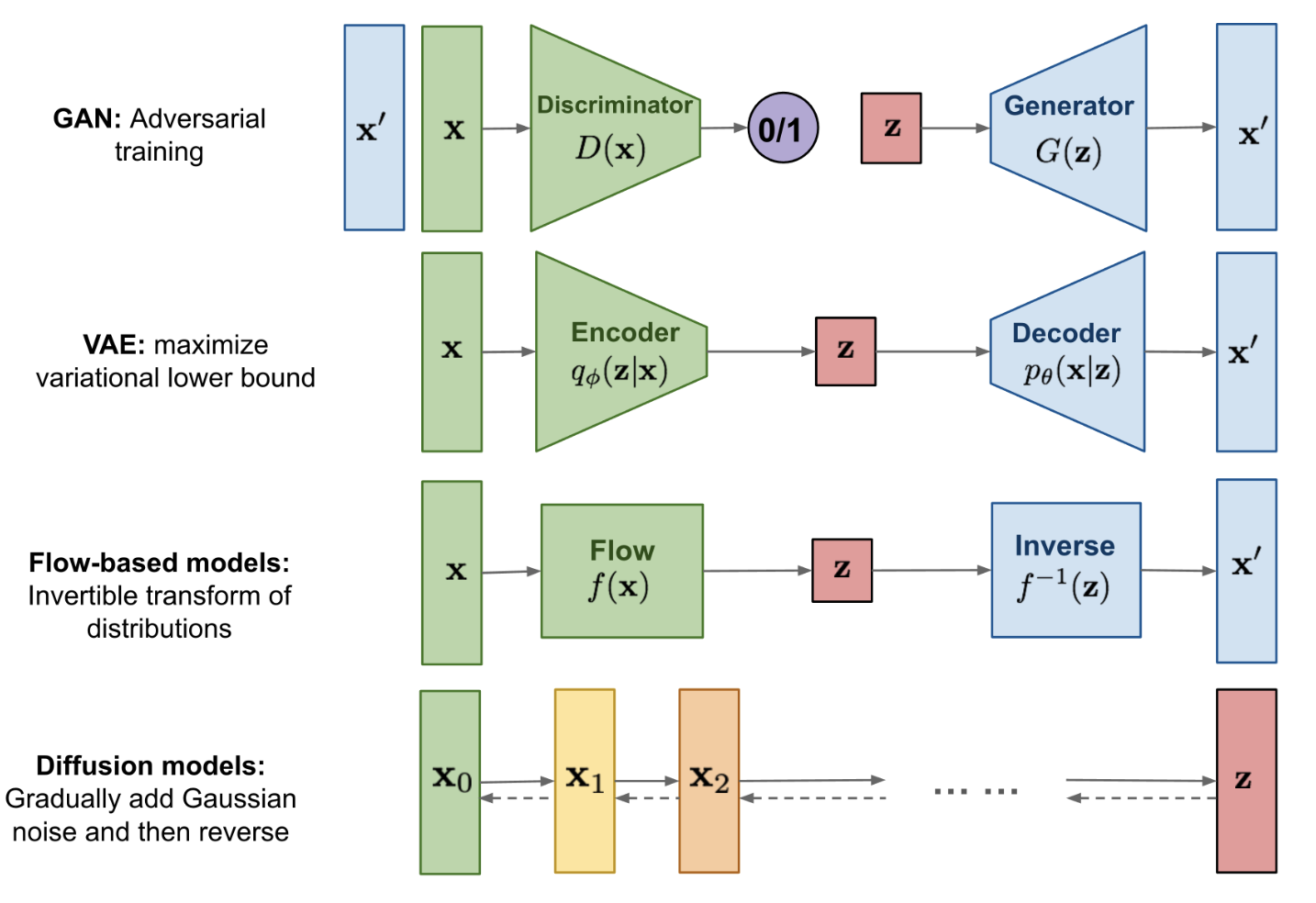
  • 图 1. 不同类型的生成模型概述。

image-20220605125755791

  1. 发展历史
  1. 快速总结
    • 优点：易处理性和灵活性是生成建模中两个相互冲突的目标。易于处理的模型可以进行分析评估并廉价地拟合数据（例如通过高斯或拉普拉斯），但它们不能轻易地描述丰富数据集中的结构。灵活的模型可以拟合数据中的任意结构，但从这些模型中评估、训练或采样通常很昂贵。扩散模型在分析上易于处理和灵活
    • 缺点：扩散模型依赖于长马尔可夫扩散步骤链来生成样本，因此在时间和计算方面可能非常昂贵。已经提出了新的方法来使该过程更快，但采样仍然比 GAN 慢。

  1. 谈谈马尔科夫：

    • 下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。
    • 转移概率矩阵：

    img

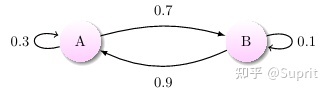
    上图中有 A 和 B 两个状态，A 到 A 的概率是 0.3，A 到 B 的概率是 0.7；B 到 B 的概率是 0.1，B 到 A 的概率是 0.9。

    img

  • ==状态转移矩阵==的稳定性

    状态转移矩阵有一个非常重要的特性，经过一定有限次数序列的转换，最终一定可以得到一个稳定的概率分布 ，且与初始状态概率分布无关。

1
2
3
4
5
6
7
8
9
10
## 状态转移矩阵
matrix = np.matrix([[0.9, 0.075, 0.025],
                    [0.15, 0.8, 0.05],
                    [0.25, 0.25, 0.5]], dtype=float)
vector1 = np.matrix([[0.3, 0.4, 0.3]], dtype=float)
## 牛 熊 横盘
for i in range(100):
    vector1 = vector1 * matrix
    print('Courrent round: {}'.format(i+1))
    print(vector1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Current round: 1
[[ 0.405   0.4175  0.1775]]
Current round: 2
[[ 0.4715   0.40875  0.11975]]
Current round: 3
[[ 0.5156  0.3923  0.0921]]
Current round: 4
[[ 0.54591   0.375535  0.078555]]
。。。。。。
Current round: 58
[[ 0.62499999  0.31250001  0.0625    ]]
Current round: 59
[[ 0.62499999  0.3125      0.0625    ]]
Current round: 60
[[ 0.625   0.3125  0.0625]]
。。。。。。
Current round: 99
[[ 0.625   0.3125  0.0625]]
Current round: 100
[[ 0.625   0.3125  0.0625]]
  • n-gram 语音识别

语言模型：N-Gram 是一种简单有效的语言模型，基于独立输入假设：第 n 个词的出现只与前面 N-1 个词相关，而与其它任何词都不相关 。整句出现的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计 N 个词同时出现的次数得到。

img

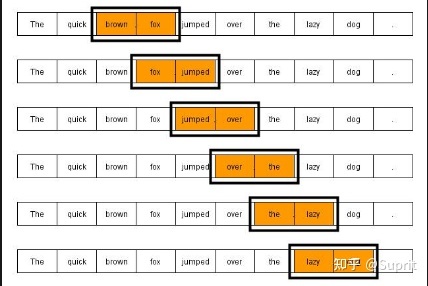
声学模型：利用 HMM 建模（隐马尔可夫模型），HMM 是指这一马尔可夫模型的内部状态外界不可见，外界只能看到各个时刻的输出值。对语音识别系统，输出值通常就是从各个帧计算而得的声学特征。

Diffusion

  • 前向扩散（逐渐加噪声）
  • 后向扩散（学会从带噪声数据中恢复内容信息）
  1. 高斯噪声：符合正态分布的噪声
    • 起伏噪声、宇宙噪声、热噪声和散粒噪声等等
    • N（μ，σ^2）
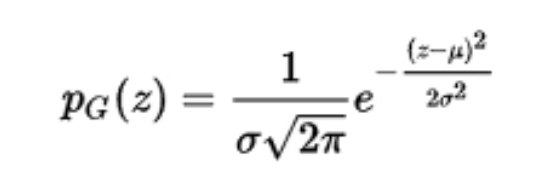
    • 高斯分布函数image-20220605134753320
  1. image-20220605135130047

  1. 高斯分布

    高斯分布可以写成以下形式：

    ![[公式]](https://www.zhihu.com/equation?tex=%5Cmathcal+N%28x%7C%5Cmu%2C%5Csigma%5E2%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%5Cleft%28+-%5Cfrac%7B%28x-%5Cmu%29%5E2%7D%7B2%5Csigma%5E2%7D+%5Cright%29)

    [公式] 是均只期望， [公式] 是方差，以上形式是基于只有一个变化维度的连续随机变量，因此以上又称为一元高斯分布。

当 [公式]时，称为标准高斯分布（标准正态分布）：

[公式]

  1. 当我们要对概率密度函数求值时，我们需要对σ平方并且取倒数。当我们需要经常对不同参数下的概率密度函数求值时，一种更高效的==参数化分布==的方式是==使用参数β∈(0,∞)==，来控制分布的精度(precision)(或方差的倒数)：

    ​ $$\frac{1}{\sigma}=\sqrt{\beta} $$

img

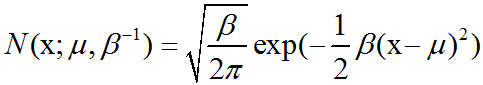
​ 正态分布可以推广到Rn空间，这种情况下被称为多维正态分布(multivariate normal distribution)。它的参数是一个正定对称矩阵∑：

img

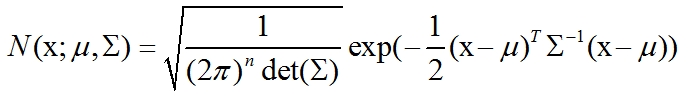
参数μ仍然表示分布的均值，只不过现在是向量值。参数∑给出了分布的 ==协方差矩阵== 。和单变量的情况类似，当我们希望对很多不同参数下的概率密度函数多次求值时，协方差矩阵并不是一个很高效的参数化分布的方式，因为对概率密度函数求值时需要对∑求逆。我们可以使用一个精度矩阵(precision matrix)β进行替代：

img

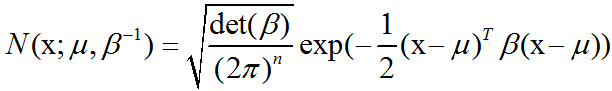
我们常常把协方差矩阵固定成一个对角阵。一个更简单的版本是==各向同性(isotropic)高斯分布==，它的协方差矩阵是一个标量乘以单位阵。